支援センター職員によるブログ

　おはようございます。がんばる中小企業と創業者を全力で支援する「広島市中小企業支援センター」の経営革新担当・久米です。

　前回の職員ブログ(2025年2月5日)では、経済効果を算出するための基礎資料（産業連関表）について説明しましたが、今回は、その資料を使った算出方法について説明します。前回、産業連関表を理解するために、簡単な取引基本表を例示しましたが、この資料をもとに「投入係数」を算出します。

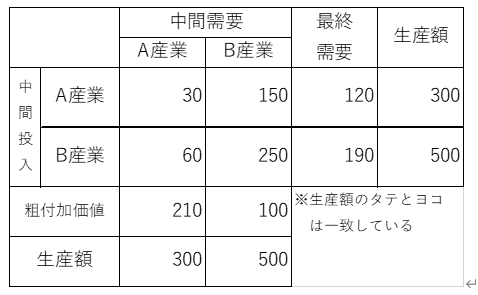
＜資料：取引基本表＞	＜資料：投入係数表＞

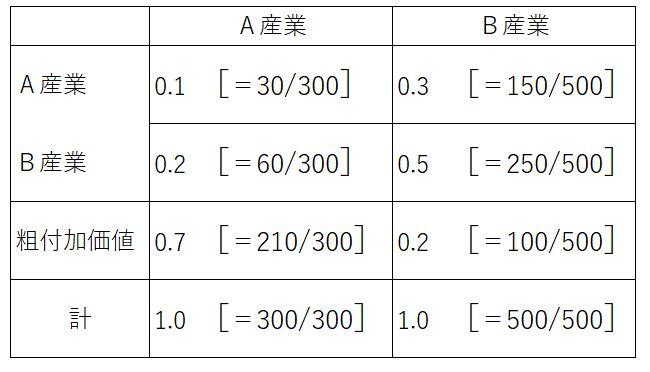※「投入係数」とは、ある産業において、１単位の生産を行う際に必要となる原材料等の単位を示したもので、中間需要のタテ(列)部門ごとに、投入額を生産額で除した数値となります。

　続いて、「逆行列係数」を算出します。

※「逆行列係数」とは、ある部門に対して新たな新規需要が１単位発生した場合に、各部門の生産(直接・間接)がどれだけ発生するか(生産波及)の大きさを示す係数をいいます。

　　　＜資料：新規需要の発生に伴う生産の波及について＞

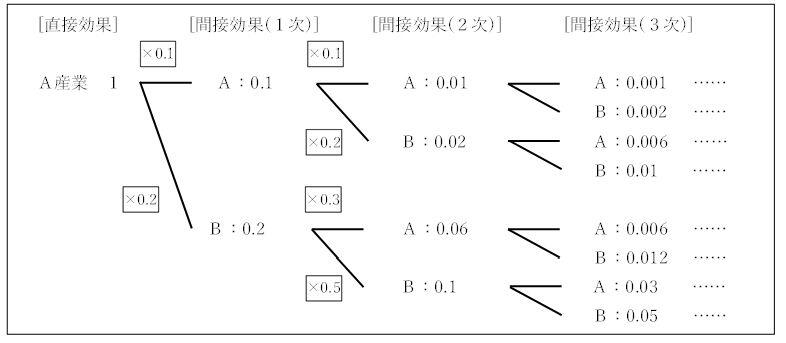
　上記表でみると、Ａ産業の新規需要が１単位発生した場合、Ａ産業そのものを１単位増加させる(直接効果)とともに、Ａ産業における生産活動で使用される原材料の投入も増加させる必要があり、Ａ産業には0.1、Ｂ産業には0.2の生産の増加 [間接効果(第1次)] が発生し、そこから更に生産の増加[間接効果(第２次)]が発生する、というように、投入係数を介した波及が続いていき、それらの数値の合計を一覧にしたものが、以下の逆行列係数表となります。

●Ａ産業への波及合計

　＝　1　＋　0.1　＋　(0.01＋0.06) 　＋　(0.001＋0.006＋0.006＋0.03)　＋　......　＝1.282

　　[直接] [間接1次] 　[間接2次] 　　　　　　　[間接3次]

●Ｂ産業への波及合計

　＝ 0.2　＋　(0.02＋0.1) ＋ (0.002＋0.01＋0.012＋0.05)　＋　......　＝0.513

[間接1次]　　[間接2次] 　　　　　　 [間接3次]

　＜資料：逆行列係数表＞

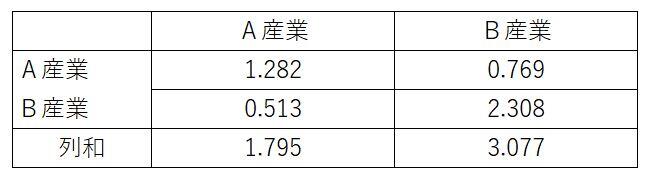
　この表では、Ａ産業に新規需要が１単位発生した場合、産業全体で1.795の波及効果を生じさせることを表しています。例えば、100億円のスタジアムを建設(A産業)する場合の経済波及効果は、179億5千万円ということになります。

　今回は理解しやすいように、Ａ産業とＢ産業の２部門のみの表で計算しましたが、実際に経済効果を算出する時に使用する産業連関表は、部門も多く影響範囲も広くなってくるものと思われます。

　なお、産業連関表による経済波及効果の算出に当たっては、どのような需要を取り入れるかなど、前提条件の設定内容で結果が変わってくることから、そのことを理解したうえで、ひとつの参考数値として見ていくのが良いかと思います。

出典：総務省ホームページ

(https://www.soumu.go.jp/main_content/000666724.pdf)